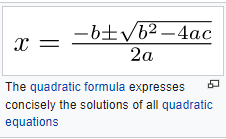MATHEMATICS
Women Graduates are trained with basics in Industry application from basic science Mathematics, Physics, Chemistry
Training in application Software by Industry Professional, to train others with preparation as TRAINER to empower.
Empowering areas are ACADEMIC SERVICE-ENTREPRENEURSHIP-DESIGN SERVICE-INDUSTRIES-SOCIAL ENGINEERING
EMPOWERING IN MATHEMATICS
Number theory began with the manipulation of numbers, that is, natural numbers 


Geometry is one of the oldest branches of mathematics. It started with empirical recipes concerning shapes, such as lines, angles and circles, which were developed mainly for the needs of surveying and architecture.
Algebra may be viewed as the art of manipulating equations and formulas. Diophantus (3rd century) and Al-Khwarizmi (9th century) were two main precursors of algebra. The first one solved some relations between unknown natural numbers (that is, equations) by deducing new relations until obtaining the solution. The second one introduced systematic methods for transforming equations (such as moving a term from a side of an equation into the other side). The term algebra is derived from the Arabic word that he used for naming one of these methods in the title of his main treatise.
Calculus, formerly called infinitesimal calculus, was introduced in the 17th century by Newton and Leibniz, independently and simultaneously. It is fundamentally the study of the relationship of two changing quantities, called variables, in the case that one depends on the other. Calculus was expanded in the 18th century by Euler, with the introduction of the concept of a function, and many other results. Presently "calculus" refers mainly to the elementary part of this theory, and "analysis" is commonly used for advanced parts.
Discrete mathematics is a recently-emerging wide area of mathematics that aggregates several existing areas that deal with finite mathematical structures and processes where continuous variations are not found. These areas have in common that, because of the discrete aspect, the standard methods of calculus and mathematical analysis do not apply directly.[c] These areas have in common that algorithms, their implementation and their computational complexity play a major role. Despite the many different objects of study, they share often similar methods.
Combinatorics may be viewed primarily as the art of enumerating a prescribed set of objects. The history of combinatorics began in ancient societies that excavated combinatorial techniques. The usage of the term combinatorics in the modern mathematical sense was coined by Leibiniz in the 17th century,[11] although Euler added many of its modern tools, such as generating functions
These subjects have belonged to mathematics since the end of the 19th century. Before this period, sets were not considered to be mathematical objects, and logic, although used for mathematical proofs, belonged to philosophy, and was not specifically studied by mathematicians.
Applied mathematics concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge. The term applied mathematics also describes the professional specialty in which mathematicians work on practical problems; as a profession focused on practical problems, applied mathematics focuses on the "formulation, study, and use of mathematical models".[citation needed]
Applied mathematics has significant overlap with the discipline of statistics, whose theory is formulated mathematically, especially probability theory. Statisticians (working as part of a research project) "create data that makes sense" with random sampling and with randomized experiments;[15] the design of a statistical sample or experiment specifies the analysis of the data (before the data becomes available). When reconsidering data from experiments and samples or when analyzing data from observational studies, statisticians "make sense of the data" using the art of modelling and the theory of inference—with model selection and estimation; the estimated models and consequential predictions should be tested on new data.[d]
Computational mathematics proposes and studies methods for solving mathematical problems that are typically too large for human numerical capacity. Numerical analysis studies methods for problems in analysis using functional analysis and approximation theory; numerical analysis broadly includes the study of approximation and discretisation with special focus on rounding errors. Numerical analysis and, more broadly, scientific computing also study non-analytic topics of mathematical science, especially algorithmic-matrix-and-graph theory. Other areas of computational mathematics include computer algebra and symbolic computation.
APPLICATION ILLUSTRATIONS
QUICKLY CREATE ACCURATE DRAWINGS FOR TEST & PRESENTATIONS